

SOLVE EQUATION SYSTEMS HOW TO
It’s helpful to use these steps when we consider how to solve systems of equations by substitution. Knowing that the solution to a system of linear equations is the point of intersection, we can confirm graphically that the coordinate pair (4,8) is the solution to this system of equations. We just solved this system of linear equations with substitution! The solution to this system is (4,8). Next, we can use the subtraction property of equality to subtract 4 from each side of the equation: Since the first equation says that x=4, we will substitute x with 4 in the second equation so that the second equation becomes: We have to decide which variable to substitute and which equation to substitute it into. Let’s start by solving the system of equations that we looked at above:Īs we decide how to solve systems of equations with substitution, we almost always have options. To solve a system of equations by substitution, we can rewrite a two-variable equation as a single variable equation by substituting the value of a variable from one equation into the other. How to Solve a System of Equations by Substitution Start practicing Algebra 1 on Albert now! Here, we will focus on how to solve a system of equations algebraically using substitution. We will cover the first two methods in other posts. The directions might say: solve by graphing, solve by elimination, or solve by substitution. When we practice solving systems of equations, students are often told which method to use to find the solution. To review how to solve equations, check out our post: Solving One-Step Equations. So, we can easily substitute that value for x into the other equation and solve for y. Let’s look at the system of linear equations below:įirst, notice we are given the value of one of the variables, x.
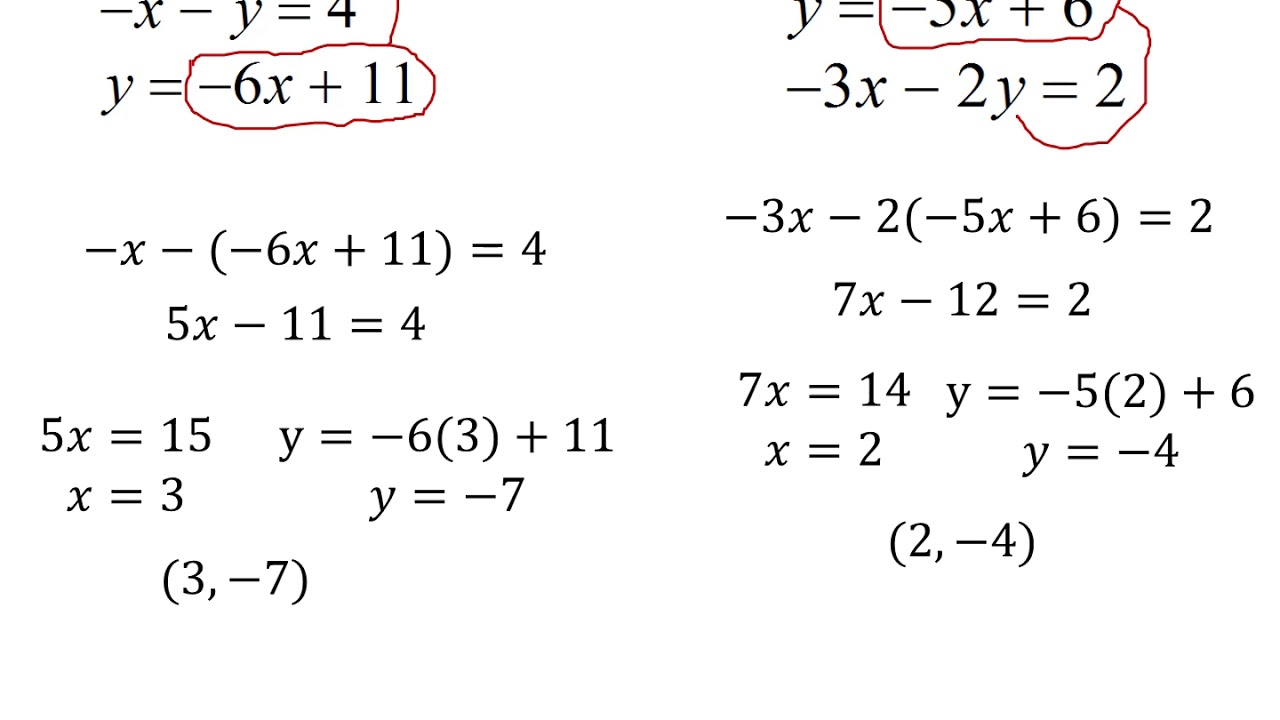
Solving systems algebraically involves manipulating the equations we are given to uncover the values of each of the variables.īut when must a system of linear equations be solved algebraically? When solving systems of equations, we should generally choose the method that takes the least effort and leaves the least room for error.

There are multiple methods for solving systems of equations, including solving systems algebraically. Solving Systems of Equations Algebraically What about situations where we have two or more variables and two or more equations? These systems of equations can seem more challenging, but solving systems of linear equations by substitution is often the easiest way to find solutions. The equation above has only one variable. There is an algebraic property of equality called the Substitution Property, which states: If x=y, then x may be replaced by y in expressions and equations.įor example, we can substitute 7 for x in the following equation. In the study of Algebra, we learn how to substitute variables for mathematical values in expressions. In each of these examples of substitution, we are replacing one entity with another equivalent one to solve a problem or reach a goal. Finally, when we run into construction on our drive home and take a different road, we’re substituting one route for another. Next, we can substitute vegan alternatives to animal products in a recipe. First, when the pitcher on a softball team hurts her shoulder, another player can take her place as a substitute. Step 6: Substitute the value from step 5 into either of the two equations and solve for the second variable.We use substitution in many situations. If you need to review, you can take a look at our article on how to solve linear equations with one variable. Step 5: Solve the equation from step 4 for the remaining variable. By doing this, we will obtain a single equation with a single variable. Therefore, we have to make one coefficient equal to a and the other equal to – a in one of the variables. We have to eliminate one of the variables when adding the equations. Step 3: Multiply one or both equations by some number, so that we obtain opposite coefficients in one of the variables. Step 2: Write the equations in the form A x+B y=C. This includes removing parentheses, eliminating fractions, and combining like terms. In detail, we can follow the following steps to solve systems of equations by elimination: The elimination method to solve systems of equations consists of multiplying one of the equations by a number, so that when adding both equations, one of the variables is eliminated. Steps to solve systems of equations by elimination


 0 kommentar(er)
0 kommentar(er)
